Here's a preview from my zine, How Integers and Floats Work! If you want to see more comics like this, sign up for my saturday comics newsletter or browse more comics!
read the transcript!
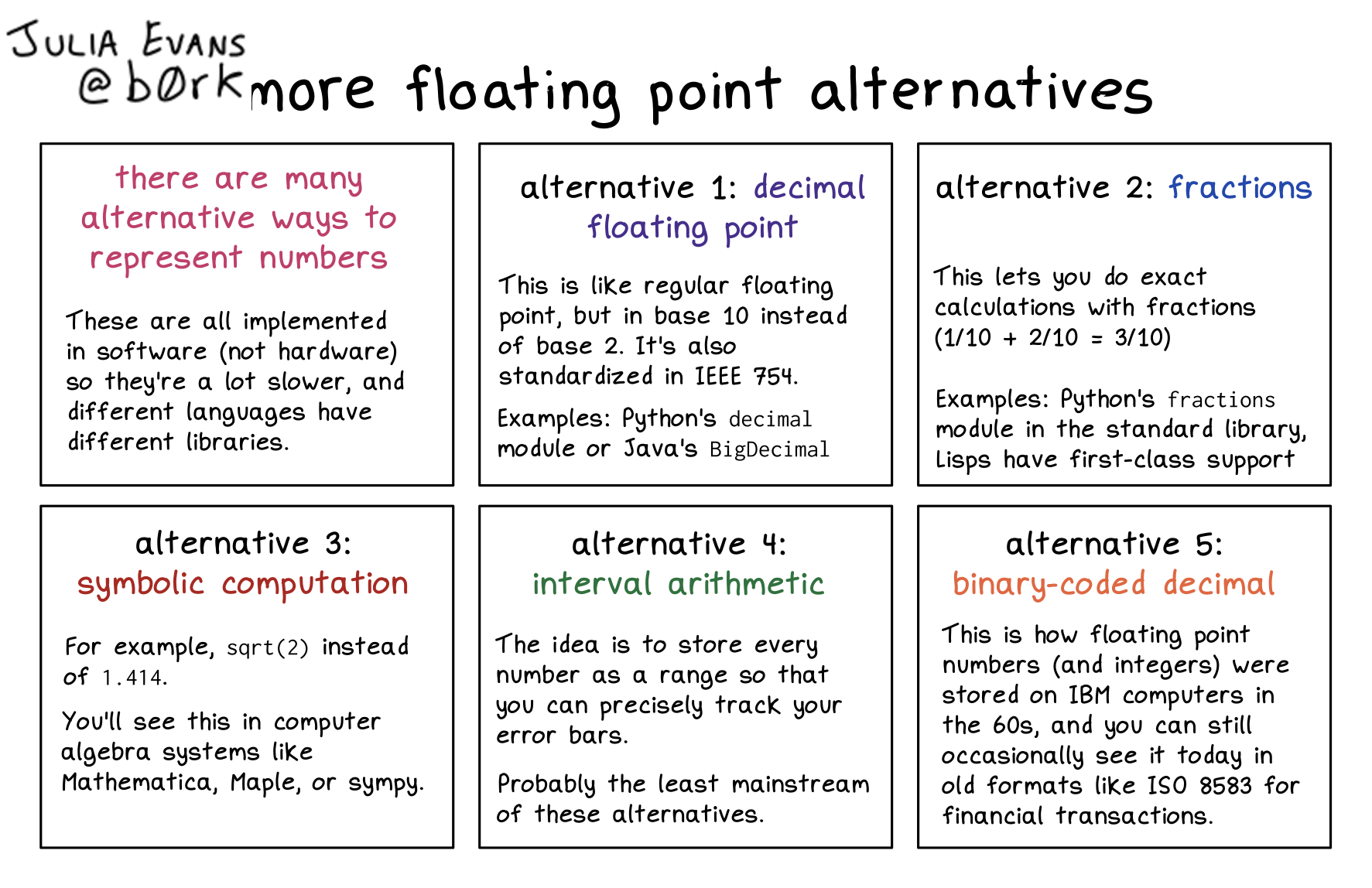
more floating point alternatives
there are many alternative ways to represent numbers
These are all implemented in software (not hardware) so they’re a lot slower, and different languages have different libraries.
alternative 1: decimal floating point
This is like regular floating point, but in base 10 instead of base 2. It’s also standardized in IEEE 754.
Examples: Python’s decimal module or Java’s BigDecimal
alternative 2: fractions
This lets you do exact calculations with fractions (1⁄10 + 2⁄10 = 3⁄10)
Examples: Python’s fractions module in the standard library, Lisps have first-class support
alternative 3: symbolic computation
For example, sqrt(2) instead of 1.414.
You’ll see this in computer algebra systems like Mathematica, Maple, or sympy.
alternative 4: interval arithmetic
The idea is to store every number as a range so that you can precisely track your error bars.
Probably the least mainstream of these alternatives.
alternative 5: binary-coded decimal
This is how floating point numbers (and integers) were stored on IBM computers in the 60s, and you can still occasionally see it today in old formats like ISO 8583 for financial transactions.
Saturday Morning Comics!
Want another comic like this in your email every Saturday? Sign up here!
