floating point math

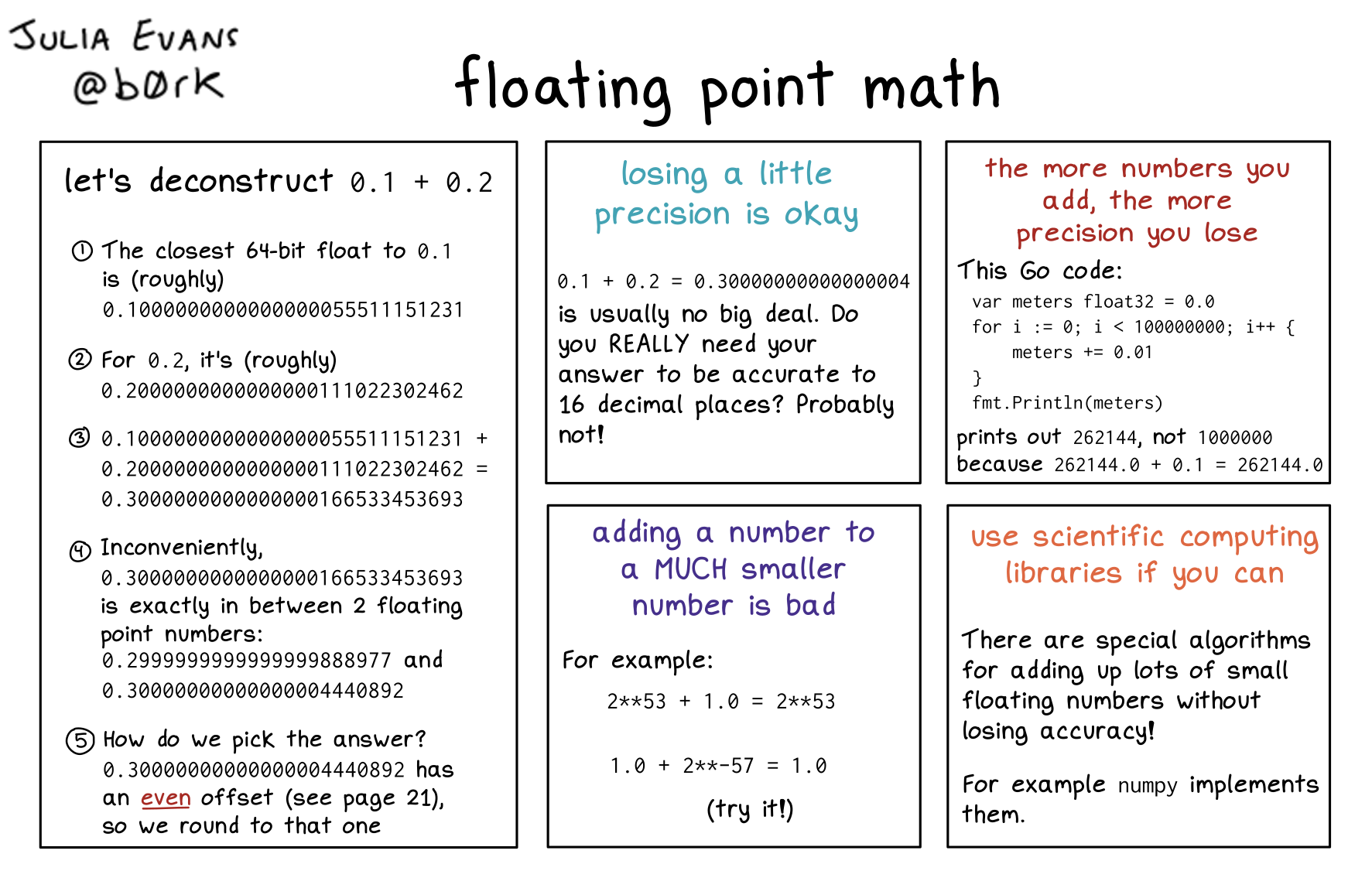
let’s deconstruct 0.1 + 0.2

1. O The closest 64-bit float to 0.1 is (roughly) 0.1000000000000000055511151231

2. For 0.2, it’s (roughly) 0.2000000000000000111022302462

3. 0.1000000000000000055511151231 + 0.2000000000000000111022302462 = 0.3000000000000000166533453693

4. Inconveniently, 0.3000000000000000166533453693 is exactly in between 2 floating point numbers: 0.2999999999999999888977 and 0.30000000000000004440892

5. How do we pick the answer? 0.30000000000000004440892 has an even offset, so we round to that one

losing a little precision is okay

0.1 0.2 0.30000000000000004 is usually no big deal. Do you REALLY need your answer to be accurate to 16 decimal places? Probably not!

the more numbers you add, the more precision you lose

This Go code:

var meters float32 = 0.0

for i = 0; i < 100000000; i++ { meters += 0.01

} fmt.Println(meters)

prints out 262144, not 1000000 because 262144.0+ 0.1 = 262144.0

adding a number to a MUCH smaller number is bad

For example:

2 xx 53 + 1.0 = 2 xx 53

1.0 + 2 xx -57 = 1.0

(try it!)

Use scientific computing libraries if you can

There are special algorithms for adding up lots of small floating numbers without losing accuracy!

For example numpy implements them.