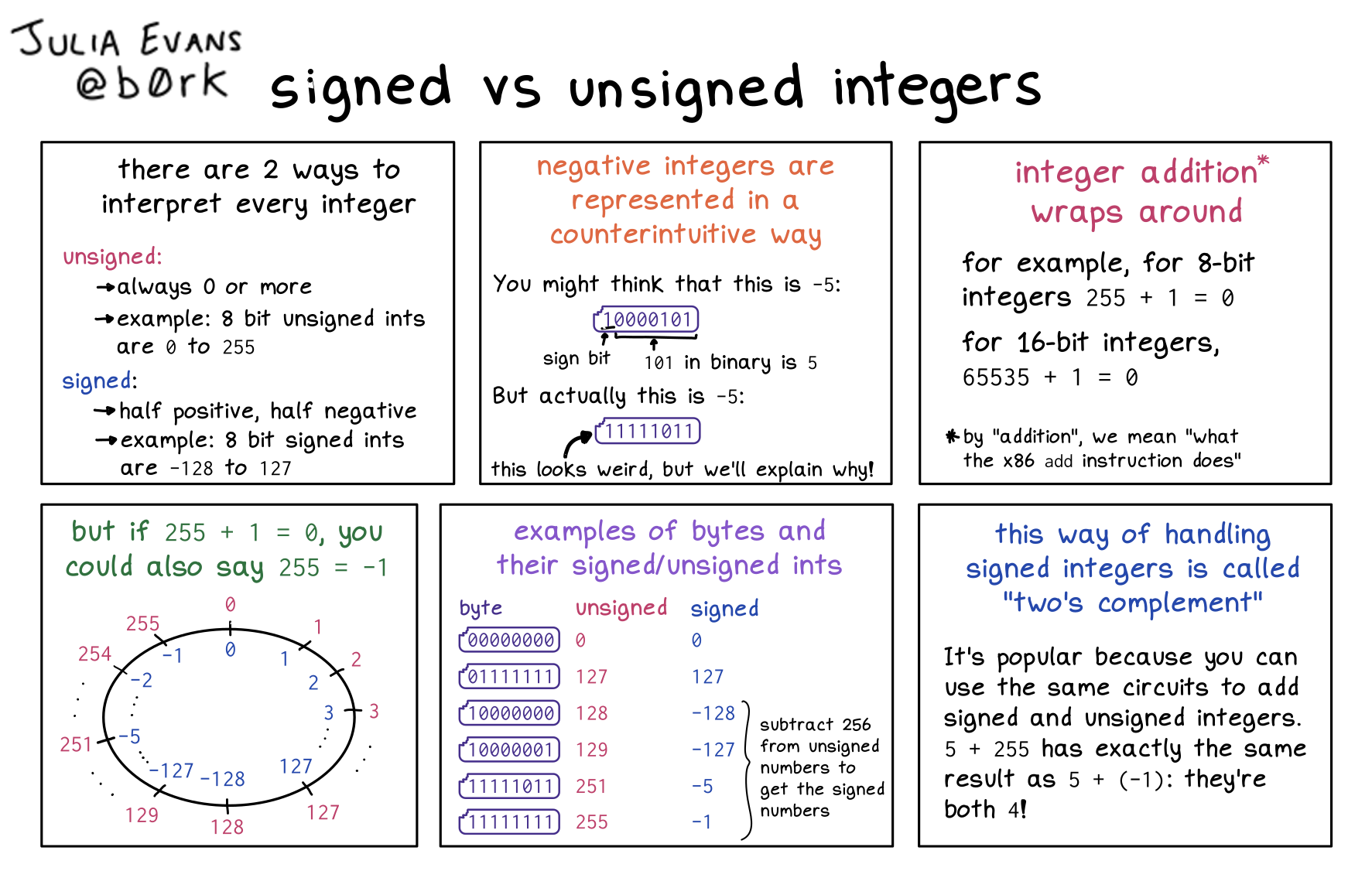
signed vs unsigned integers

there are 2 ways to interpret every integer

unsigned: - always 0 or more - example: 8 bit unsigned ints are 0 to 255

signed: - half positive, half negative - example: 8 bit signed ints. are -128 to 127

negative integers are represented in a counterintuitive way

You might think that this is -5: 10000101

(1 is the sign bit, and 101 in binary is 5)

But actually this is -5: 11111011

this looks weird, but we’ll explain why!

integer addition wraps around

for example, for 8-bit integers 255 + 1 = 0

for 16-bit integers, 65535 + 1 = 0

by “addition”, we mean “what the x86 add instruction does”

panel:

but if 255 + 1 = 0, you could also say 255 = -1

examples of bytes and their signed/unsigned ints

subtract 256 from unsigned numbers to get the signed numbers

this way of handling signed integers is called “two’s complement”

It’s popular because you can use the same circuits to add signed and unsigned integers.

5 + 255 has exactly the same result as 5 + (-1): they’re both 4!