panel 1:

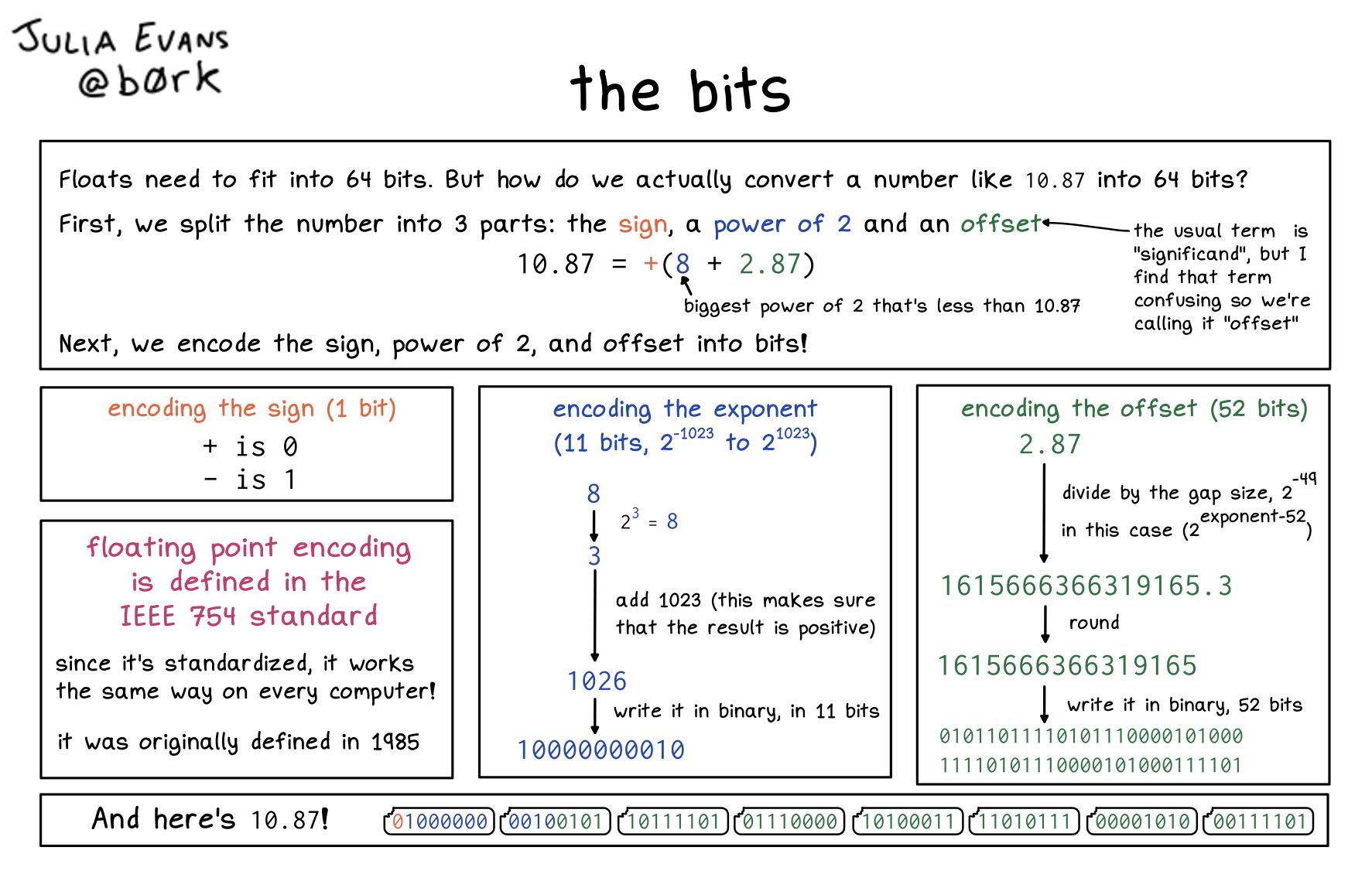
Floats need to fit into 64 bits. But how do we actually convert a number like 10.87 into 64 bits?

First, we split the number into 3 parts: the sign, a power of 2 and an offset

(The usual term is “significand”, but I find that term calling it “offset”)

10.87 = + (8 + 2.87)

(8 is the biggest power of 2 that’s less than 10.87)

Next, we encode the sign, power of 2, and offset into bits!

encoding the sign (1 bit)

+ is 0

- is 1

floating point encoding is defined in the IEEE 754 standard

since it’s standardized, it works the same way on every computer!

it was originally defined in 1985

encoding the exponent (11 bits, 2^-1023 to 2^1023)

8

↓ 2^3 = 8

3

↓ add 1023 (this makes sure that the result is positive)

1026

↓ write it in binary, in 11 bits

10000000010

encoding the offset (52 bits)

2.87

↓ divide by the gap size, 2^-49

in this case (2^exponent-52)

1615666366319165.3

↓ round

1615666366319165

↓ write it in binary, 52 bits

01011011110101110000101000

11110101110000101000111101

And here’s 10.87!

01000000 00100101 10111101 01110000 10100011 11010111 0001010 00111101